正在加载中，请稍后
author 首页 关于 笔记

按回车搜索更多
用 Java 解数学题之 <老师在纸上写了两个正整数... >
2021-06-09 阅读 {{counts.readCount}} 评论 {{counts.commentCount}}

前言

老师在纸上写了两个正整数，
把它们的和告诉了小红，
把它们的积告诉了小明。 老师说：这两个正整数可能相等也可能不相等。
1. 小明说：我不知道这两个数是多少。
2. 小红说：我也不知道这两个数是多少。
3. 小明说：我现在知道了。 请问这两个数到底是多少？

原题如上，是在某个b站up主的视频里看到的
我是感觉这题非常适合写成代码让计算机来算
说干就干，用java8实现了一个基础草率版本的算法



折腾

先简单还原一下现场过程

小明得到4，可以拆分出 1 x 4 或者 2 x 2
这里可能出现的答案明显不唯一
故问1， 小明回答，不知道

假设这里能通过，小明得到的只能是素数
比如小明拿到3 必然马上拆分出是 1 x 3
这里没通过，也说明小明必然没拿到素数

小红得到5，可以拆分出 1 + 4 或者 2 + 3
套娃小明分析得出 1 x 4 = 4 ， 2 x 3 = 6
4和6都不是素数，都存在可能，答案明显不唯一
故问2， 小红回答，不知道

最后小明个zz回答知道了
这只存在一种可能，就是小明套娃小红套娃小明后，所有的可能性里，只存在一个分支，是小红不知道，其余小红必知道。
回到数学上，刚才说
小明是4，分析自己可以是 1 x 4 或者 2 x 2
套娃小红后 小红只能是 1 + 4 = 5 或者 2 + 2 = 4
如果小红是 5
可以分析成 1 + 4 = 5 或者 2 + 3 = 5
套娃小明后得出 1 x 4 = 4 或者 2 x 3 = 6
如果小红是 4
可以分析成 1 + 3 = 4 或者 2 + 2 = 4
套娃小明后得出 1 x 3 = 3 或者 2 x 2 = 4
这种情况是绝对不可能出现的，因为如果小明是3
第一回合，小明必知道自己是 1 x 3 或者 3 x 1
所以如果小红是4，第二回合能直接排除掉1 和 3，只能是2 和 2
小红说不知道，所以小红也必不可能是 4
那么小红只能是5， 1 + 4 = 5 或者 4 + 1 = 5
小明个zz就知道了



说的有点啰嗦，反正就是这个意思，下面上代码



先上个基础款

  1. package com.company;
  2. 

  3. 

  4. /**
  5.  * 原题
  6.  * 老师在纸上写了两个正整数，
  7.  * 把它们的和告诉了小红，
  8.  * 把它们的积告诉了小明。
  9.  * 老师说：这两个正整数可能相等也可能不相等。
  10.  * 1. 小明说：我不知道这两个数是多少。
  11.  * 2. 小红说：我也不知道这两个数是多少。
  12.  * 3. 小明说：我现在知道了。
  13.  * 请问这两个数到底是多少？
  14.  *
  15.  * 思路
  16.  * 结合 1，说明小明得到的数字 分解成 x * y 可能性不唯一
  17.  * 结合 2，说明小红得到的数字 分解成 x + y 再结合成 x * y 结果依旧不唯一
  18.  * 结合 3，说明小明得到的数字 分解成 x * y 再结合成 x + y 可以得到多个结果，但只有一个小红不能唯一，其余结果小红在2中必能解开
  19.  */
  20. 

  21. public class Main {
  22. 

  23.     /**
  24.      * 判断是否为素数
  25.      */
  26.     public static boolean isPrime(int number) {
  27.         for (int i = 2; i < number; i++) {
  28.             if (number % i != 0) {
  29.                 continue;
  30.             }
  31.             return false;
  32.         }
  33.         return true;
  34.     }
  35. 

  36.     /**
  37.      * 排除不合格的数字b
  38.      * 拆解b 后模拟乘 不为素数的可能性必须大于2
  39.      */
  40.     public static boolean checkNumberB(int number) {
  41.         int count = 0;
  42.         for (int i = 1; i <= number / 2; i++) {
  43.             int x = i;
  44.             int y = number - i;
  45.             if(!isPrime(x * y)){
  46.                 count ++;
  47.             }
  48.         }
  49.         return count < 2;
  50.     }
  51. 

  52.     /**
  53.      * 能进入这里说明不是素数
  54.      * 拆解a 后模拟加
  55.      */
  56.     public static boolean checkNumberA(int number) {
  57.         int count = 0;
  58.         for (int i = 1; i <= Math.sqrt(number); i++) {
  59.             // 能整除
  60.             if(number % i == 0){
  61.                 int x = i;
  62.                 int y = number / i;
  63.                 // 核心就是这句话 套娃
  64.                 if(checkNumberB(x + y)){
  65.                     count ++;
  66.                 }
  67.             }
  68.         }
  69.         // a这个数字拆分完 模拟完 只允许出现一个能通过的可能性 否则都不符合问题3
  70.         return count != 1;
  71.     }
  72. 

  73.     /**
  74.      * 核心算法
  75.      */
  76.     public static void core() {
  77.         for (int i = 1; i < 100; i++) {
  78.             for (int j = 1; j < 100; j++) {
  79.                 int a = i * j;
  80.                 int b = i + j;
  81.                 // 对应问题1 a 不能是素数
  82.                 if (isPrime(a)) {
  83.                     continue;
  84.                 }
  85.                 // 对应问题2 b 拆分后模拟 i*j所有可能性能通过验算
  86.                 if(checkNumberB(b)){
  87.                     continue;
  88.                 }
  89.                 // 对应问题3 略
  90.                 if(checkNumberA(a)){
  91.                     continue;
  92.                 }
  93.                 // 上面3个逻辑排除完 还没被排除的就是正确答案 i 和 j 就是那2个数，a 是积，b 是和
  94.                 System.out.println("i = " + i + " , j = " + j + " , a = " + a + " , b = " + b);
  95.             }
  96.         }
  97.     }
  98. 

  99.     public static void main(String[] args) {
  100.         core();
  101.     }
  102. }



运行结果如下

  1. i = 1 , j = 4 , a = 4 , b = 5
  2. i = 4 , j = 1 , a = 4 , b = 5

上述代码已得到正确答案，但我设置的范围是100以内，如果数字设置过大，运算复杂度高，会非常缓慢。当然我也能估计出来，可以用数学的方法，来证明只存在这一组答案，不需要计算大范围。但我还是想锻炼一下我的AMD 4800H CPU，所以这里再加上多线程试试



代码如下

  1. package com.company;
  2. 

  3. 

  4. import java.util.concurrent.ExecutorService;
  5. import java.util.concurrent.Executors;
  6. 

  7. /**
  8.  * 原题
  9.  * 老师在纸上写了两个正整数，
  10.  * 把它们的和告诉了小红，
  11.  * 把它们的积告诉了小明。
  12.  * 老师说：这两个正整数可能相等也可能不相等。
  13.  * 1. 小明说：我不知道这两个数是多少。
  14.  * 2. 小红说：我也不知道这两个数是多少。
  15.  * 3. 小明说：我现在知道了。
  16.  * 请问这两个数到底是多少？
  17.  * <p>
  18.  * 思路
  19.  * 结合 1，说明小明得到的数字 分解成 x * y 可能性不唯一
  20.  * 结合 2，说明小红得到的数字 分解成 x + y 再结合成 x * y 结果依旧不唯一
  21.  * 结合 3，说明小明得到的数字 分解成 x * y 再结合成 x + y 可以得到多个结果，但只有一个小红不能唯一，其余结果小红在2中必能解开
  22.  */
  23. 

  24. public class Main {
  25. 

  26.     /**
  27.      * 判断是否为素数
  28.      */
  29.     public static boolean isPrime(int number) {
  30.         for (int i = 2; i < number; i++) {
  31.             if (number % i != 0) {
  32.                 continue;
  33.             }
  34.             return false;
  35.         }
  36.         return true;
  37.     }
  38. 

  39.     /**
  40.      * 排除不合格的数字b
  41.      * 拆解b 后模拟乘 不为素数的可能性必须大于2
  42.      */
  43.     public static boolean checkNumberB(int number) {
  44.         int count = 0;
  45.         for (int i = 1; i <= number / 2; i++) {
  46.             int x = i;
  47.             int y = number - i;
  48.             if (!isPrime(x * y)) {
  49.                 count++;
  50.             }
  51.         }
  52.         return count < 2;
  53.     }
  54. 

  55.     /**
  56.      * 能进入这里说明不是素数
  57.      * 拆解a 后模拟加
  58.      */
  59.     public static boolean checkNumberA(int number) {
  60.         int count = 0;
  61.         for (int i = 1; i <= Math.sqrt(number); i++) {
  62.             // 能整除
  63.             if (number % i == 0) {
  64.                 int x = i;
  65.                 int y = number / i;
  66.                 // 核心就是这句话 套娃
  67.                 if (checkNumberB(x + y)) {
  68.                     count++;
  69.                 }
  70.             }
  71.         }
  72.         // 只能存在一个通过套娃 checkNumberB 的结果
  73.         return count != 1;
  74.     }
  75. 

  76.     /**
  77.      * 核心算法
  78.      */
  79.     @SuppressWarnings("AlibabaThreadPoolCreation")
  80.     public void core(int nThreads) {
  81.         ExecutorService executorService = Executors.newFixedThreadPool(nThreads);
  82.         for (int i = 1; i < 1000; i++) {
  83.             for (int j = 1; j < 1000; j++) {
  84.                 executorService.submit(new CalcThread(i,j));
  85. 

  86.             }
  87.         }
  88.         executorService.shutdown();
  89.     }
  90. 

  91. 

  92.     public static void main(String[] args) {
  93.         // 开200个线程去跑
  94.         new Main().core(200);
  95.     }
  96. 

  97.     class CalcThread extends Thread {
  98.         private int i;
  99.         private int j;
  100. 

  101.         public CalcThread(int i , int j){
  102.             this.i = i;
  103.             this.j = j;
  104.         }
  105. 

  106.         @Override
  107.         public void run() {
  108.             int a = i * j;
  109.             int b = i + j;
  110.             // 对应问题1 a 不能是素数
  111.             if (isPrime(a)) {
  112.                 return;
  113.             }
  114.             // 对应问题2 b 拆分后模拟 i*j所有可能性能通过验算
  115.             if (checkNumberB(b)) {
  116.                 return;
  117.             }
  118.             // 对应问题3 略
  119.             if (checkNumberA(a)) {
  120.                 return;
  121.             }
  122.             // 上面3个逻辑排除完 还没被排除的就是正确答案 i 和 j 就是那2个数，a 是积，b 是和
  123.             System.out.println("i = " + i + " , j = " + j + " , a = " + a + " , b = " + b);
  124.         }
  125.     }
  126. }



注意我这里开200个线程还能正常操作，如果你的电脑CPU不太能经受得起锻炼，少开点线程试试水，开个16线程足以


运行结果如下

  1. i = 1 , j = 4 , a = 4 , b = 5
  2. i = 4 , j = 1 , a = 4 , b = 5



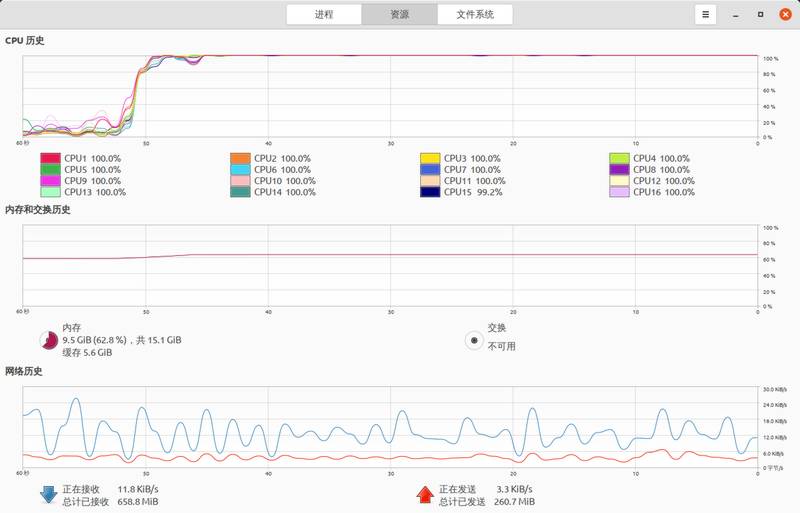
最后运行结果还是意料之中的，但cpu曲线图异常的优美，另外温度也很感人。速度的话远不及预期，可能是因为数字越大，越卷。。。

END

提交
评论区空空如也，赶紧添加一条评论吧 评论 {{counts.commentCount}}
{{comment.name}} {{comment.os}} {{comment.browser}}
{{dateFormatter(comment.createTime)}}

{{comment.message}}

{{comment.reply.name}} {{comment.reply.os}} {{comment.reply.browser}}
{{dateFormatter(comment.reply.createTime)}}

{{comment.reply.message}}

 zzzmh
关于我 留言板

网址导航
{{alert.message}}
留言板 * 站长不经常查看信箱 若有重要事宜联系邮箱 admin@zzzmh.cn 取消 发送
云朵 ChungZH 起航天空 yiranzai 前端大爆炸 Web前端之家 前端博客 shirmy 小宁博客 pdbn LOGI 鄢云峰 边界AI
Copyright © 2024 上海藏原羚工作室 沪ICP备18011999号 沪公网安备31010602005070号
微信公众号